天赋数感•大脑可塑
摄影：中央大学认知与神经科学研究所助理教授张智宏
采访许碧纯
婴儿天生有数感，知道一加一等于二。 然而，大脑何以能形成抽象的数学概念？如何应付书写的文字和数字？ 当共通的基本认知能力和后天文化建构而成的能力相互竞争时，大脑有何策略？ 《科学人》特别专访以研究数感成名的法国认知神经科学家狄昂。
狄昂是法兰西学院实验认知心理学教授、巴黎国家卫生暨医学研究院认知神经造影研究部主任，主要的研究是数字认知、阅读的神经机制以及双语学习。 他原主修数学和资讯科学，因为不想成为一名研究数学的学者，却发觉数学思考是大脑最奇特的心理历程之一，于是转攻认知科学，师承知名认知科学家也是《天生婴才》的作者梅勒（Jacques Mehler）。 狄昂在2005年以40岁年纪获选为法国科学院院士，2010年获选为美国科学院院士。 发表专业论文之外，也着有多本科普书，他目前最有兴趣的研究议题是意识。科学人：我们的第一个问题是关于你在1997年出版的《数字感》（The NumberSense）这本书，它应该是认知心理学中第一本有系统描绘人类数学认知的书籍。
狄昂：这是很好的起头，因为我刚好就在今年夏天开始修订《数字感》，预计明年4月出版。 新版会新增一个很长的结尾篇章，内容包含了过去15年的研究进展。
这真是太好了！ 我们的读者可以得到第一手资讯。 其实这也跟我们的问题有关，你在这本书中对数感天赋论举出许多实验证据，特别是对于大脑如何处理数量讯息，提出了概算和精算两种策略，并证实负责这两个处理历程的神经机制。 这些年来在大脑数学认知方面有什么新发现或突破吗？
狄昂：据我所知，其实有很多新的进展和突破。 其中最重要的是如同过去行为实验结果所预期的，动物脑中有负责辨别数量的神经元。 这是由德国杜宾根大学的奈德（Andreas Nieder）和他在美国麻省理工学院的合作者进行的一项出色研究，显示动物脑中的神经元对特定的数量有很大的反应。美国伊利诺大学的罗伊特曼（JDRoitman）、杜克大学的布赖农（EMBrannon）与普莱特（ML Platt）这组人的研究则显示，动物脑中的神经元会随着数量的变化而有递增或递减的反应。 这些研究最令人着迷的地方在于思考如何用数字感的理论去解释这些神经元的运作，它们分别说明了动物有数感，也有概算数量的能力。
另一个重要的突破是研究者试图了解儿童如何发展出数字感。 美国哈佛大学史培基（ Elizabeth S. Spelke ）的研究指出，数感这项婴儿天生就有的能力，跟他们长大后在学校学习算术的能力有很高的相关性。 我们也有许多直接的研究证据说明，数字感如何在儿童学习算术的早期发展过程中提供学习的鹰架。
在这个领域里，有很多研究取向是从动物身上得到初步结论后，再放到人类去做重复验证，或是反过来进行。 我和义大利特伦托大学的皮亚查（Manuela Piazza）利用神经元有适应转变的特性，以功能性磁共振造影（fMRI）技术来显示人类大脑和动物一样，都有对数量变化特别敏感的神经元。
「数」虽然是很抽象的概念，但认知心理学家很早就已证实婴儿有简单的算术能力，只是数不过三，研究显示，这项运算最多只达到四。
整体说来，我们对于大脑概算数量的神经回路已有相当的了解。 现阶段最大的挑战是去了解人类大脑如何在与生俱来、负责处理数字感的神经回路上，建立学习数学的神经系统。
顶叶与数学能力之谜
你方才提到的突破之一是儿童的概算能力与他们未来学习算术的能力相关。 有任何关于数字认知的理论可以解释为什么有些人天生对数学很在行而有些人碰到数学就竖起白旗？ 拥有优异数学能力的孩子是因为他们天生就有较好的数字感吗？
狄昂：这是很好的问题，但是我对这种说法抱持非常谨慎的态度。 一篇发表在《自然》的论文指出，概算能力与孩子早期在学校学习算术的能力有相关，反之亦然，皮亚查和我的研究也显示，被诊断为有计算障碍的儿童在概算能力与数量知觉的作业上表现异常，而且他们在概算非数字符号呈现的点（dot）时，也会出现困难。 有许多研究证据显示，人类对于非数字符号的数量处理与学习高等数学的能力有关。 还有一个发表在《美国国家科学院学报》的脑造影研究显示，数学能力的发展和顶叶与额叶之间的神经连结程度有很高的相关。这些研究的共同问题是，实验结果只显示了数学能力好与不好的人之间脑部的差异，我们仍然不知道数学能力发展和顶叶与额叶的神经连结之间是否有因果关系。
不过，如果大脑顶叶在出生前就有损伤，那么似乎会导致发展性计算障碍，英国伦敦大学的艾萨克斯（ElizabethIsaacs）在2001年的研究发现，顶叶灰质数量比正常发展的婴儿还少的早产儿，长大后会有发展性计算障碍，研究中所指的顶叶正是一般人用来处理数学相关作业的脑区。同样地，因染色体缺失导致透纳氏症候群的孩子也无法执行某些算术作业。
对于部份（我必须特别强调并非所有）的儿童而言，我们相信大脑顶叶与数学能力的学习是有因果关系的。 但这一类发展性研究必须面临的共同问题是因果螺旋关系，而这正是我们需要更进一步去理解的，意思是说，从生物学角度来看，个体最初的极小遗传差异，虽会导致往后发展的极大困难，但教育的介入可以使那些数学学习困难的孩子得到很有效的协助。 基因或许扮演了一些角色，但单凭基因并不足以构成数学天份的基础。
[经典实验]婴儿天生会数数
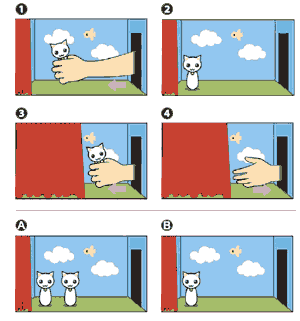美国耶鲁大学心理学教授温恩1992年发表在《自然》上的经典研究显示，四、五个月大的婴儿会期待一加一等于二。 在这个小玩偶戏台上，首先研究人员将一个玩偶放在舞台上空手离去，留下玩偶在舞台上（１和２），然后布幕打开，再放进第二个，空手离开（３和４）。 当布幕打开时，有时舞台上呈现两个玩偶（Ａ），有时则只有一个（Ｂ另一个由研究人员偷偷取走），结果显示，婴儿理解一加一等于一的时间要比一加一等于二所花的时间长；研究者也进行另一组实验二减一，结果也发现婴儿理解二减一等于二所花的时间要长于二减一等于一。
婴儿认知能力的研究在过去20年突然增加许多，你认为引发新一波婴儿研究的原因是什么？ 是因为有了更好的研究工具和方法？ 有更好的理论让研究者以此为基础去问更多问题？ 还是有更健全、更完整的婴儿大脑发展资料库可以验证许多研究假说？
狄昂：我想上述原因都成立，但我认为更重要的是对智识来源的追寻。 认知科学领域的一个核心问题在于试图了解人类从哪里来？ 我们为何可以形成抽象概念？ 特别是数学概念的产生是一个很奥妙的现象，例如我们有直线或平面的概念，但它们却是我们无法从外在世界体验到的绝对抽象概念。 这是从柏拉图就开始探寻的古老哲学问题。 令人兴奋的是，透过研究婴儿的大脑及其行为，我们可以开始用实证的方式重新探索这个议题。
另外，我认为这些研究背后的主要动力在于，我们虽然拥有很多关于成人大脑的知识，但对于婴儿的大脑却一无所知，一旦有技术可以进行婴儿大脑的研究，是让每个研究者都感到非常兴奋的。 就在几个月前，法国国家科学研究中心伊瑟德（Véronique Izard）的研究显示，出生几个小时的新生儿就可以经由视觉和听觉的配对，得知物体或声音所表达的数量讯息。 我们不断从婴儿行为中发现他们所拥有的能力，这是令人非常兴奋的，那表示我们呱呱坠地来到这个世界时，便具有一些基本的认知能力，而它正是柏拉图过去猜想也宣称的论点。
来自初生婴儿的神经造影证据
在我们访问之前，曾经寄给你贾布尼克的文章，其中提到婴儿可以从接收到的刺激中发掘规律性变化，你对于这种统计学习理论有何看法？ 它与你所称的婴儿天生的认知能力是否有关联性？
数感从何而来？
60年前德国神经学家发现，左下顶骨皮质如果受损可能导致计算力缺失和书写困难等障碍， 狄昂和合作者柯恩（Laurent Cohen）在一些左下顶骨皮质受损的病患身上也看到丧失数字感 的相同情形，而此区很可能就是与生俱来数感的地方。 在此图中，左右大脑都具有数量概 念和阿拉伯数字的辨识能力，但只有左大脑有数字的语言表达。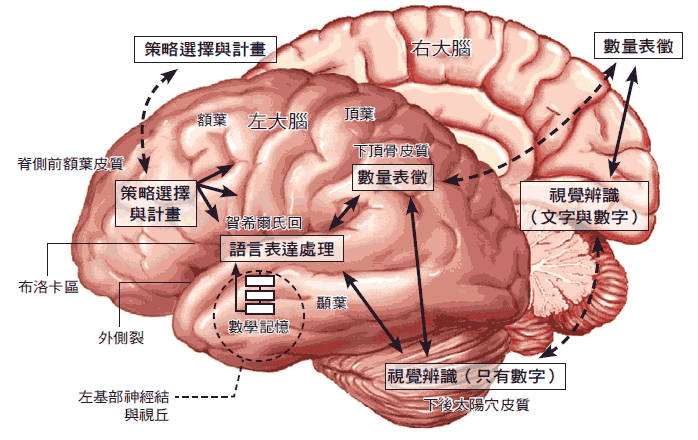
狄昂：针对后面的那个问题，我的答案是否定的。 有研究显示婴儿可以很快速地学习新的事物，这是毫无疑问的。不仅是人类，即使是动物脑中的神经系统都能有效地提取外在环境中的规律性变化，并以此对外在世界可能的变化做出预测。 当我们听一连串短暂的语音，我们的大脑可以发掘其中的规律性，并以此预测将来可能的变化，这是事实，的确是我们所擅长的，它因此让研究者形成有趣的推测，认为人类大脑会去预期一些具有规律性的机率，并从中做出推论。 但是大脑提取规律性的能力并不足以解释大脑如何形成数量、空间和时间的表征或拥有语言的能力，因为婴儿接触到的刺激不足以让他们学习。
前面提到的发展性研究，受试婴儿才出生几个小时，我不认为他们有足够的经验，让他们可以从环境中形成抽象的数量表征。 比较可能的解释是，婴儿脑中原本就存在着一个有组织的神经系统，让他们很早就开始有数量的概念。 的确，我和我的太太吉丝兰（Ghislaine Dehaene-Lambertz,狄昂–林巴狄斯）一起研究婴儿大脑的神经连结发现，这些连结并非随机形成，脑区间连结的组织性也比我们想像的更强，因此我们认为数量表征或语言能力是来自大脑中系统性的连结，而不只是因为提取规律性的统计学习能力。
我最喜欢举的例子是同时刊登在《自然》上的两篇研究，英国伦敦大学的勃吉斯（Neil Burgess）以及挪威科技大学的穆瑟（Edvard Moser）两个独立研究团队分别透过老鼠脑细胞的研究发现，幼鼠在还不太能走动时，场所细胞（place cell）、网格细胞（grid cell）及头部方位细胞（headorientation cell）就已经存在脑中了。他们的研究最精采之处在于显示这些尚未开始在空间中进行探索的幼鼠，其大脑就已经展现系统性的神经组织，虽然还不是很完善，但这些细胞如同脑中的指南针一般，让老鼠知道自己正朝着什么方向移动。 因此这些幼鼠并不是因为学习，而是脑中与生俱来的神经系统让它们具有方向感。
我不认为我们应该过份强调「与生俱来」这一点，但如同美国耶鲁大学温恩（Karen Wynn）所说，我们似乎天生就具备了一些基本能力，如数字感和空间感。 从这个立基点开始，人类当然还有非常特殊的学习能力，其中之一是使用符号，例如以阿拉伯数字计算物体的个数，也因为具备了这些基本能力，人类发展出比其他动物更高等的认知功能。 基本能力是存在的，没有必要否认。
你提到了语言的基本能力，你也与狄昂–林巴狄斯使用fMRI来研究婴儿语言习得的历程，能否请你谈谈这方面的最新发展？
狄昂：这类实验的进行是非常困难的，你可以想像：包括找小婴儿来当受试者、只能在晚上做实验、如何让他们在仪器中头不会乱动……我们要解决许多这类的问题。 虽然我们在2002年发表了第一篇论文，但仍然有很多困难需要解决，例如婴儿移动头部的问题。
不过，还是有一些有趣的研究进展，其中之一是我们非常清楚地在两个月大婴儿的脑中观察到，从左颞叶、布洛卡区开始一路延伸到额叶的神经回路，都对语音有活化反应。 不仅如此，这条神经回路的组织方式与脑区对语音活化的反应速度有关，活化反应最快的是贺希尔氏回（Heschl's gyrus），接着是颞叶，最慢的是布洛卡区，这又是一个显示脑功能具有组织特性的例子。
大脑提取规律性的 能力并不足以解释 大脑如何形成数 量、空间和时间的 表征或拥有语言的 能力，因为婴儿接 收到的刺激不足以 让他们学习。
另一个新实验显示，两个月大婴儿的左侧贺希尔氏回对语音的活化反应较大，而右侧则对音乐的活化反应较大。这与过去行为实验说明婴儿可以分辨言语与音乐的结论是一致的，而且我们观察到外侧裂（perisylvian）周围语言区的神经网络在婴儿牙牙学语之前就 启动了。
这些研究结果意味着这条神经回路在婴儿出现言语行为之前，就已经是处理言语的专化系统，然而我们还不确定这个神经系统是为了语言而演化出来，还是为了一般的听觉处理而演化出来，然后被重新用来处理语言的刺激？ 这是未来要解答的问题。
再现大脑可塑性：人脸与文字辨识共争同一脑区
Scientific American -Mind今年初针对你刚出版的Readingin the Brain做了篇你的专访。 有趣的是，你在《数字感》中强调婴儿与生俱来的数量概 念，但是在Reading in theBrain里，却从脑的观点探讨非自然的阅读行为。 你能否从脑部发育的角度，比较数学和阅读在学习历程上有何异同之处？
狄昂：这是一个很棒的问题！ 我认为学习数学和阅读的共通点在于，它们一部份是立基于基本认知能力，一部份是后天文化建构出来的。 以阅读为例，我们的大脑并非为了学会阅读而演化来的，文字在5000年前才发明出来，直到最 近几个世纪前，还只有少部份的人有机会识字，在这么短的时间内，阅读行为并不能导致基因或大脑结构的改变，但是阅读会对发育中的大脑带来改变。 为了阅读，我们将原本负责物体辨识的神经系统转而做为辨识字母形状的系统。
我们惊讶地发现，人类在阅读中文、法文或从右到左的希伯来文时，无论是阅读拼音字母还是意符文字，都在同一个脑区出现活化反应，也就是视觉字形区（visual wordform area）。 这个脑区成为我们学会文字与说话的连结之后的介面，我们发现它也对简单形状，像是交叉形状、类似桌角或人类的脚，以及膝盖部位的L形或T形都有活化反应。 我认为它是动物共有的物体辨识神经系统，而因为这个系统具有可塑性，能适应并处理不同的新形状，人类大脑便将它转为处理与辨识文字的系统。
大脑为因应阅读这个后天文化建构出来的能力，而将原本负责物体辨识 的视觉神经系统转为辨识字母形状，显示大脑的可塑性，也证实了学会 阅读带给大脑的改变，对大脑正在发育的学龄孩童尤为重要。
就在两周前，我们有一篇研究文盲大脑的论文被《科学》接受。 我们比较了会阅读与不会阅读的人的大脑，发现这两组人在大脑中展现的主要差异正是在视觉字形区，这个区域活化的程度会随着阅读经验而增加，而它对非文字形状（如棋盘状）的刺激，以及对人脸的刺激，反应都有下降的趋势，这似乎暗示着不同种类的刺激在同一脑区的竞争关系。
我们认为这是因为文字辨识与人脸辨识运用了大脑皮质中非常相近的区域，当这个脑区被用来处理其中一种刺激时，就会降低对另一种刺激的活化反应。 虽然这个现象造成的效果量很小，但仍具统计的显著性。 这个发现的意义在于证实大脑会挪出皮质的资源，来支援学习新的文化能力，学会阅读这件事明显改变了我们的大脑。
在上述的专访中，你提到认知发展的生物性限制（bio-logical constraint），它指的是遗传、神经亦或行为层次的限制？ 能否请你针对「大脑神经元的重新利用」（neuronal recycling）多做解释并举例说明？
对大脑正在发育的学龄儿童来说，学校教育取代了演化的角 色，不需要透过基因改造，在短短几周或几个月内，就为孩子 的大脑带来改变。
狄昂：古尔德（Stephen Jay Gould）对物种演化提出了外推（extrapolation）的想法，即一个原本为了某种功能而演化出来的系统，后来可能转而负责另一个功能或目的，典型的例子是熊猫的拇指。 我的理论也用了相似的概念，但是不涉及基因的改变，如同之前所言，阅读行为的发生时间不足以导致基因的改变，实际的情况是，对一个大脑正在发育的学龄儿童来说，学校教育取代了演化的角色，不需要透过基因改造，在短短几周或几个月内，就对孩子的大脑带来改变。
人类大脑的特殊之处在于能利用原有的神经系统发展出新的功能，人类文化的建构就是在这个过程中产生的。 我想强调的是，许多文化发明其实是重新利用原有的系统进而创造出新功能的结果。 以面具为例，法国尼寇研究中心的斯波伯（Dan Sperber）认为，在所有的文化中都可以发现面具或化妆等文化产物，这是因为人脑中有个处理人脸的刺激的神经模组，于是我们经常创造出一些超常刺激来兴奋这个神经模组。 漫画中人物夸张的脸部表情对于这个神经模组也有同样效果，不过作用不如一张实际的人脸来得好。 我们在这些超常刺激中得到乐趣，同时也使得这种新的产物在文化中被保留下来。
亚洲文化具计算优势？
有些研究指出，文化与语言在数学能力上发挥重要的作用，例如中文和日语。 以中文来说，最重要的因素是中文数字词汇的语法结构可以直接对应到十进位的结构，同时也对应到阿拉伯数字的书写格式，中文数字符号系统只有13个独立符号，即数字「一」至「九」，以及「十」、「百」、「千」、「万」；也因此，使用者比较容易学习十进位制。
另一个文化差异是利用算盘所做的训练，算盘是相当有趣的工具，它利用可移动的算珠来模拟计数的概念，是一种非符号的表达方式，是数学教学上很好的辅助教材。 由狄昂实验室开发的一套「数学竞赛」（Number Race）软体，已经有多国语版，可以帮助儿童发展数字感、学习数量和空间对应关系、数量符号，以及学习十进位的结构，而灵感正是来自于算盘。（文╱许碧纯）
我认为阅读行为也具有相似情况，我们重新利用视觉系统，让它以有效率的方式和言语系统形成连结，而因为学会识字这件事会有很多用处，因此能够稳定地成为文化的一部份。
假设不同文化下的婴儿大脑都同样有与生俱来的能力，你认为针对婴儿的认知能力进行跨文化比较的重要性为何？
狄昂：准确地说，我们的目的是区分什么是共同的基本认知能力，什么又是后天文化建构的结果？ 让我们回头来谈数量认知的研究。 我们曾在亚马逊河流域进行一系列心理学实验，当然是行为实验，因为那里没有任何脑造影仪器。 亚马逊孟杜鲁古人（Mundurucu）的特别之处在于，他们不仅没有到学校念过书或学过算术，在他们语言中也没有词汇用来表示超过五的数字，我们试图研究这些人如何表征数量概 念，有两个有趣的发现。
首先，即使他们没有词汇表达六以上的数量，他们跟我们一样可以概算3040个点的数量，显示概算能力是人类共有的基本能力。 其次，我们也观察到文化间的具体差异，对我们而言，数字具有线性的特性，「1」接下来是「2」，「2」的下一个是「3」，它们之间是等距的。 也就是说，「1」和「2」的间距与「8」和「9」的间距相等，因此数量可以用来测量空间。 但是孟杜鲁古人没有线性数量的概念，对他们来说，「1」和「2」之间的距离比「8」和「9」之间的距离远，意即「1」和「2」是不同的数量，但「8」和「9」则是相似的数量。 显示线性数量的概念其实是来自文化的建构。 我认为这是一个很好的例子，可以说明什么是人类共有的基本认知能力，什么又是文化带来的差异。
作者
许碧纯是《科学人》杂志特约记者。
本文感谢阳明大学神经科学研究所乙组学生洪意惠的协助。
延伸阅读
《数字感》，狄昂（Stanislas Dehaene）着，王丽娟译，先觉出版，2000年。
〈陌生的一、二、三、四、五……〉，《科学人》，2009年3月号。
Numerical Values Leave a Semantic Imprint on Associated Signs in Monkeys , IlkaDiester, Andreas Nieder. Journal of Cognitive Neuroscience, Vol. 22, page 174–183;January, 2010.
Monotonic Coding of Numerosity in Macaque Lateral Intraparietal Area , Jamie D.Roitman et al, PloS Biology , Vol. 5, Issue 8, e208; August, 2007.
Non-symbolic Arithmetic Abilities and Mathematics Achievement in the First Year ofFormal Schooling . CK Gilmore et al, Cognition , Vol. 115, 394-406; March, 2010.
Individual Differences in Non-verbal Number Acuity Correlate with MathsAchievement . Justin Halberda et al. Nature , Vol.455, page 665-668; October 2,2008.
How Learning to Read Changes the Cortical Networks for Vision and Language.Stanislas Dehaene et al, Science , November 11 (online), 2010.
www.psychspace.com心理学空间网
